Quantum computer, towards a next technological revolution?

How does a quantum computer work?

If you don't understand, you are beginning to understand...

Just like a "classical" computer, the quantum computer uses bits (1 or 0). But these bits have the particularity to react to the principles of quantum physics. They are called q-bit (quantum bit). The q-bit can be represented by the spin of an electron, the polarization of a photon, etc.

Scientists exploit two fundamental principles of quantum physics that give full (exponential) computing potential to q-bits:

1. Superposition of states: the spin of an electron, for example, is in a superposition of states (spin-up 👍, spin-down 👎), meaning it is in both states at the same time, with a probability of appearance for each of them.
2. Quantum entanglement: if 2 particles are entangled, the measurement of the first allows to induce the second's without even measuring it, no matter how far apart they are. In that case, those 2 particles are part of a single state.

Thanks to these 2 principles, scientists are able to obtain phenomenal computing powers:

• Let's take 2 bits (classical): this gives a system with 4 possible states (00, 01, 10, 11), but there are, at a given time, only 2 possible values (0 or 1 for the first bit, 0 or 1 for the second).
• Let's take 2 q-bits (quantum): this gives a system with 4 states too, except that all the states exist at each given time thanks to the principle of superposition.
• Let's take 300 q-bits: this gives a system with 2^300 states, which is more than the total number of particles in the universe!

On the other hand, q-bits are also governed by the wave function collapse, which requires, when measuring the q-bit, that it is in one of these so-called ground states (👍 or 👎). In addition, all information about the superposition state of the q-bit is lost, forever...

Despite all, scientists can exploit q-bits by leveraging quantum algorithms, composed of quantum logic gates, that interfere on the quantum state (superpositions) to converge towards a solution.

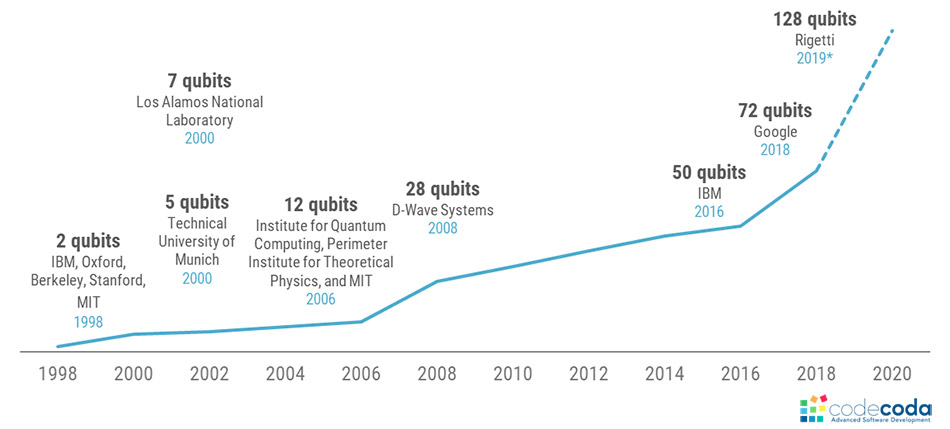
More and more q-bits

• 2009: Yale created the first 2 q-bit quantum processor
• 2016: IBM created a 50 q-bit processor
• 2019: Google created Sycamore, a 54 q-bit quantum processor, enabling them to achieve quantum supremacy
• 2023: IBM promises a 1000 q-bit quantum computer!

Practical applications of quantum computers

As of today, the practical applications are still limited because there are very few equivalents in terms of quantum algorithms to solve concrete problems. Nevertheless, the potential is real.

Prime number factorization - 🦖 = 🐑 + 🐑 + 🐑 + 🐑 + ... + 🐑

In 1994, the mathematician Peter Shor discovered a quantum algorithm for prime number factorization whose computational performance is much better than that of the best classical algorithm, respectively O(log n) and O(√n).

In terms of web security, this raises a real problem, because most of the current cryptographic algorithms (RSA, etc.) are based on this prime number factorization principle. But in practice, the "quantum supremacy" of Shor's algorithm is still a rather distant dream. It is estimated that it would take:

• 2000 error-free q-bits (impossible in practice)
• 1 billion q-bits with error

Nevertheless, the quantum computer could well allow the arrival of new cryptographic algorithms more robust and more powerful.

Unsorted list search quantum algorithm - 🔎 ( 🍅 🥔 🍅 🍅 🥔 🥔 🍆 )

In 1996, Lov Grover, another mathematician, discovered a quantum algorithm allowing the search in an unsorted list with, again, performances far better than the best current algorithm (respectively O(√n) and O(n/2)).

Complex optimization problems

There are many complex optimization problems, such as determining the shortest path between two points in a network.

Due to the fact that quantum processors enable a very large number of parallel calculations, they are particularly interesting for solving these types of problems.

In 2019, Volkswagen launched the first pilot project for the optimization of the (real time) bus network of the city of Lisbon, thanks to the quantum system of D-Wave, one of the major players in the field of quantum computing, specialized in optimization problems (quantum annealing).

Simulation problems

Quantum computers also have real potential for simulation problems, such as:

New drug synthesis: simulate all possible reactions of a drug on the human body before its commercialization.

Quantum system simulation: what better solution than a quantum computer to simulate the quantum world and better understand it?

Human brain simulation: simulating the vast complexity of neurons/synapses in a human brain for better medicine (fun fact: in 2013, researchers were only able to simulate 1% of the human brain using the most powerful computer at the time!)

The potential of quantum computers is now proven, but their application is still experimental, which is mainly due to the fact that they are still complicated to operate (cooled down to about absolute 0), that they still generate too many errors and that there are very few quantum algorithms to solve concrete problems. It is also very unlikely that they will one day supplant classical computers, because they depend a lot on them to be able to operate (especially for error correction). Nevertheless, we can imagine, in the long run, cloud services allowing us to execute part of a (complex) calculation on quantum systems, on demand.